nim game과 grundy number를 익히기 전에 이와 같은 필승 전략 게임이론이 적용되기 위한 전제조건부터 알아보자.
Impartial game
두 플레이어가 게임을 하는데 아래 조건을 만족해야 한다.
- 모든 정보가 공개된 게임
- 두 플레이어가 할 수 있는 행동이 같은 게임
첫 번째 조건으로 포커 같은 게임은 해당되지 않는다. 모든 정보가 공개되어있지 않고, 서로 상대의 패를 모르기 때문이다.
두 번째 조건으로 바둑, 체스 같은 게임도 해당되지 않는다. 각자 자신의 돌(흑/백), 말(킹, 퀸, 비숍...)만 움직일 수 있으니 할 수 있는 행동이 다르기 때문이다.
다시 조건을 해석해보면 선공/후공만 다를 뿐 이를 제외한 조건은 모두 같은 게임을 칭한다. 빡빡한 조건으로 이런저런 게임들이 다 해당되지 않으면 무슨 게임이 있을까?
가장 기본적으로는 배스킨라빈스 31 게임이 해당된다. 누가 먼저 시작하냐만 다를 뿐 현재 숫자에서 최대 +3까지 외칠 수 있는 동일한 조건이기 때문이다. 배스킨라빈스 31의 필승법은 조금만 생각해도 알 수 있겠지만 좀 더 문제가 어려워지면 필승법을 찾기란 쉽지 않다.
Nim game
대표적으로 nim game이 impartial game에 해당된다.

nim game이란 여러 더미가 주어지고 각 더미에 여러 구슬이 들어있는 상태에서 번갈아가면서 게임을 진행한다.
각 플레이어가 할 수 있는 행동은 다음과 같다.
- 여러 더미 중 하나의 더미를 선택한다.
- 선택한 더미에서 한개 이상의 구슬을 가져온다.
이를 반복할 때 구슬이 없어서 못 가져오는 플레이어가 지는 게임이다. 위에 설명한 impartial game의 두 가지 조건이 모두 충족되는 것을 확인할 수 있다.
그럼 이 게임의 필승법을 알아보자.
nim game 필승법
$$s = d_1\oplus d_2\oplus ...\oplus\ d_n$$
$d_i$는 i번째 더미에 있는 구슬의 개수이다. 모든 구슬의 수를 xor 한 $s$가 0보다 크면 선공, 0이면 후공하면 항상 이길 수 있다. 뜬금없이 xor이 나왔지만 아래 두 가지 정리를 보면 명확해진다.
- $s$가 0이면 다음 차례에는 0이 될 수 없다.
- $s$ 식에서 어느 하나의 $d_i$값이 달라지면 s도 달라진다.
- $s$가 0보다 크면 다음 차례에 항상 0으로 만들 수 있다.
- 첫번째 비트가 가장 큰 $d_i$에서 제거하면 가능한 $s$의 모든 값을 만들 수 있다.
따라서 필승을 하기 위해 처음 더미가 주어질 때 모든 구슬을 xor 해서 $s$를 구한다. $s$가 0보다 크면 선공을 통해 $s$를 0으로 만들고, $s$가 0이라면 후공을 통해 상대가 $s$를 0이 아닌 수로 만들게 하는 전략을 사용하면 항상 이길 수 있다.
grundy number
grundy number는 nimber라고도 불리는데 nim game과 비슷하게 필승 전략을 짜는 방법이다. 이번에도 예제 게임으로 전략을 알아보자.
2 x n 게임판이 있고, 번갈아 가면서 게임을 진행한다. 각 플레이어는 1x1 또는 2x2의 정사각형을 하나씩 색칠할 수 있는데, 모든 칸이 색칠되어 더 이상 진행할 수 없는 플레이어가 지는 게임이다. 이때 X 표시된 칸에는 색칠할 수 없다.
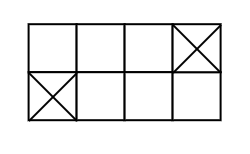
예를 들어, 위와 같은 게임판이 주어진다면 선공을 통해 가운데 2x2를 색칠한다면 이길 수 있다. 어떤 게임판이 주어질 때 필승법을 grundy number를 통해 구해보자.
grundy number는 다음과 같이 정의한다.
$$G_{state} = mex({G_{state'}\ |\ state'\ 는\ state의\ 다음\ 상태})$$
mex는 minimum excluded number로 해당 집합에 존재하지 않는 가장 작은 수를 뜻한다. $G_{state}$를 구하기 위해서는 다음 상태들의 grundy number를 알아야 하고, 다음 상태 역시 그다음 상태의 grundy number를 알아야 한다. 재귀적으로 들어가다가 최종적으로 모든 게임판이 색칠되면 $G_{모두\ 색칠된\ 상태} = 0 $으로 정의한다.
그러면 위와 같은 게임판의 grundy number를 구하는 과정은 아래 그림과 같을 것이다.

가장 상위에 있는 우리가 원하는 상태의 다음 상태인 7가지에 대해서 grundy number가 {3, 1, 1, 1, 1, 3, 0} 이기 때문에 이 중에 존재하지 않는 가장 작은 수인 2가 현재 상태의 grundy number가 된다.
grundy number 필승법
grundy number를 구했으니 이게 무슨 의미이고, 어떤 전략을 세울 수 있는지 생각해보자.
- 현재 상태의 grundy number가 0이면 다음 상태에는 0이 존재하지 않는다.
- 현재 상태의 grundy number가 0이 아니면 다음 상태에는 0이 존재한다.
이를 바탕으로 nim game과 비슷하게 필승 전략을 세울 수 있다.
- 현재 상태의 grundy number가 0이면 후공을 통해 상대가 0을 깨뜨리도록 만든다.
- 현재 상태의 grundy number가 0이 아니면 선공을 통해 0으로 만든다.
이런 전략을 세우면 내 차례에는 항상 grundy number가 0이 아니고, 상대 차례에는 항상 0 이도록 강제할 수 있다. 번갈아 가며 게임을 진행하다 마지막 상태에 이르면(grundy number = 0) 상대 차례가 되고, 나는 항상 승리할 수 있다.
subgame이 여러 개 있는 grundy number
이번에는 같은 규칙인데 게임판이 여러 개 있는 경우의 필승법을 알아보자.

마찬가지로 번갈아 가면서 어느 게임판 하나를 골라서 1x1 또는 2x2를 색칠할 수 있다. 이때의 필승법은 grundy number와 nim game을 합친 것과 비슷하다. 모든 게임판의 grundy number를 구해서 xor 한 값이 0보다 크면 선공, 0이면 후공을 하면 된다.
$$ ans = G_{state_1} \oplus\ G_{state_2} \oplus\ ...\ \oplus\ G_{state_n}$$
정리
nim game과 grundy number에 대한 이해를 바탕으로 다양한 게임 문제를 적절한 모델링을 통해 적용시킬 수 있다. 참고로 grundy number 문제 예시로 들은 정사각형 칠하는 게임은 https://www.acmicpc.net/problem/1603 에서 채점할 수 있다.
'알고리즘' 카테고리의 다른 글
| 중국인의 나머지 정리(Chinese remainder theorem) (0) | 2019.10.18 |
|---|---|
| 포함과 배제, 그리고 뫼비우스 함수 (0) | 2019.10.18 |
| 투셋(2-sat) (0) | 2019.10.18 |
| Manacher's Algorithm (0) | 2019.10.17 |
| 고속 푸리에 변환(FFT, Fast Fourier Transform) (1) | 2019.10.17 |




댓글