이전 글(푸리에 변환)에서 이산 푸리에 변환(DFT)과 역변환(IDFT), 그리고 그 이점에 대해서 정리했었다.
다른 분야에서도 널리 쓰이겠지만 PS에서 그 용도만 다시 정리해보면 어떤 수열들에 대해 복잡한 연산(예를 들어 convolution)을 할 때, DFT로 변환 후 연산을 하고 IDFT로 역변환을 해서 결괏값을 얻을 때 사용한다. 한 번에 할 것을 세 번(DFT, 연산, IDFT)에 하기 때문에 비효율처럼 보이지만 복잡한 연산이 변환 후 수열에서는 간단한 연산으로 바꿀 수 있어서 훨씬 효율적이다.
어떻게 간단한 연산으로 대체되는지는 이전 글에서 확인 가능하고, 이번 글에서는 변환/역변환을 빠르게 하는 방법을 알아보자.
Discrete Fourier Transform (DFT)
$ a_{n} $의 이산 푸리에 변환 $ A_{n} $은 다음과 같다.
$$ A_{n} = \sum_{j=0}^{N-1} e^{-2 \pi ijn/N} a_{j} $$
오일러 공식때문에 복잡해 보이니 $ E(x) = e^{-2 \pi ix} $ 를 이용해보자.
1의 주기를 가지며 지수 연산의 특성을 가진 $ E(x) $ 는 $ E(x+y) = E(x)\times E(y) $ 과 같은 특징이 있고 아래 유도할 때 이 성질이 사용된다.
$$ \begin{align} A_{n} &= \sum_{j=0}^{N-1} E(\frac{jn}{N})\ a_{j} \\
&= \sum_{j=0}^{\frac{N}{2}-1} E(\frac{(2j)n}{N})\ a_{2j} + \sum_{j=0}^{\frac{N}{2}-1} E(\frac{(2j+1)n}{N})\ a_{2j+1} \\
\\
&= \begin{array}{c}{\sum_{j=0}^{\frac{N}{2}-1} E(\frac{jn}{\frac{N}{2}})\ a_{2j} + E(\frac{n}{N}) \sum_{j=0}^{\frac{N}{2}-1} E(\frac{jn}{\frac{N}{2}})\ a_{2j+1} \ \ \ \ \ (n < \frac{N}{2})} \\{\sum_{j=0}^{\frac{N}{2}-1} E(\frac{jn}{\frac{N}{2}})\ a_{2j} - E(\frac{n}{N}) \sum_{j=0}^{\frac{N}{2}-1} E(\frac{jn}{\frac{N}{2}})\ a_{2j+1} \ \ \ \ \ (n \geq \frac{N}{2})} \end{array} \end{align} $$
$ A = \{A_0, A_1, A_2, A_3, ... , A_{N-1}\} $ 을 두 개로 나눠보자.
- $ A_{even} = \{A_0, A_2, A_4, ...\} $
- $A_{odd} = \{A_1, A_3, A_5, ...\} $
짝수항과 홀수항을 나눠서 생각해보면 마지막 식은 결국 $A_n = A_{even, n} \pm E(\frac{n}{N}) A_{odd,n} $ 이다. 즉, 길이 n짜리 DFT A는 길이 $ \frac{N}{2} $짜리 $A_{even}, A_{odd}$ 두 DFT를 알고 있다면 n번의 연산만에 구할 수 있고 따라서 총 시간 복잡도는 $ O(Nlog_2N) $ 이 된다.
$$ T(n) = 2 \times T(\frac{n}{2}) + n $$
Inverse Discrete Fourier Transform (IDFT)
이번엔 IDFT를 빠르게 구해보자. 원래 식은 다음과 같다.
$$ a_n = \frac{1}{N} \sum_{j=0}^{N-1} e^{2 \pi ijn/N} A_{j} $$
DFT와 마찬가지로 $ E(x) = e^{-2 \pi ix} $ 를 이용해보자.
$$ a_n = \frac{1}{N} \sum_{j=0}^{N-1} E(\frac{-jn}{N})\ A_{j} $$
식을 보면 DFT와 매우 비슷하다. 다만 $ E $ 에 들어가는 j의 부호가 바뀌고 결과값을 N으로 나눠주는 게 추가되었다. 이 두가지만 따로 처리하면 나머지 로직은 DFT와 동일하다.
FFT 구현
Cooley-Tukey 알고리즘으로 간결하게 구현할 수 있다. 위 방법에서 살펴봤듯이 재귀적으로 절반의 크기를 구하기 때문에 기본적으로 수열의 길이를 $ 2^N $으로 맞춰놓고 시작한다.
$A$를 구하기 위해 $A_{even}, A_{odd}$를 구해서 연산을 해도 충분히 빠르지만, 매번 이에 해당하는 메모리를 할당해야 하는 문제점이 있다.
예를 들어 $A = \{A_0, A_1, A_2, A_3, A_4, A_5, A_6, A_7\}$ 를 생각해보자.
이를 구하기 위해 $A_{even} = \{A_0, A_2, A_4, A_6\}$과 $A_{odd} = \{A_1, A_3, A_5, A_7\}$ 를 메모리를 할당해서 구할 테고, 또 이를 구하기 위해 재귀적인 메모리 할당이 반복될 것이다. 이를 그림으로 보면 다음과 같다.
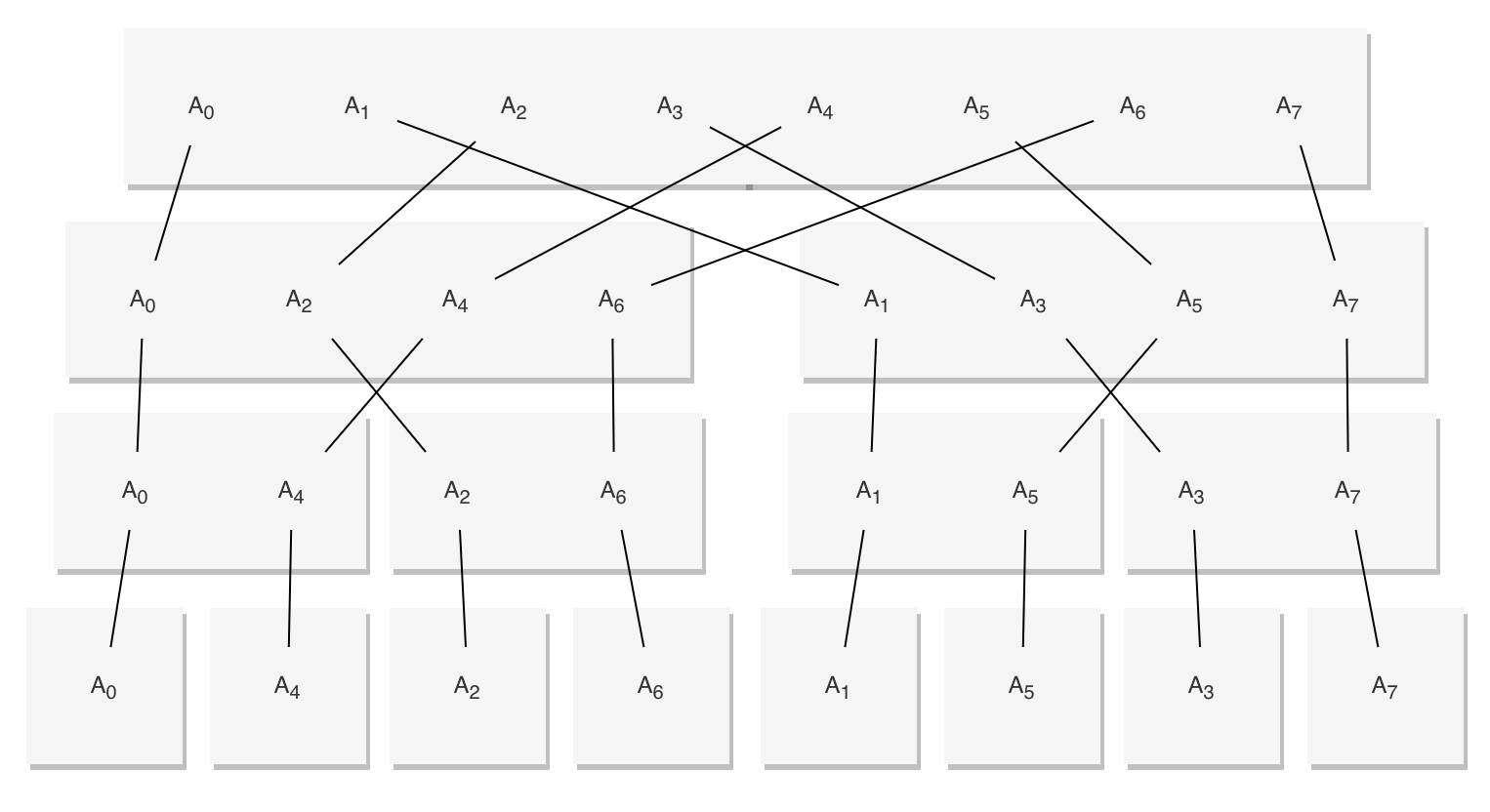
이렇게 총 $O(Nlog_2N)$의 메모리가 소요된다.
하지만 역으로 생각해보면 애초에 $ A = \{A_0, A_4, A_2, A_6, A_1, A_5, A_3, A_7\} $ 을 담고 있으면 요리조리 왔다 갔다 할 필요 없이 이웃한 수열끼리만 연산을 하면 된다. 이웃한 수열끼리 연산을 한다면 even과 odd를 합치는 과정에서 추가적인 메모리 할당없이 현재 메모리를 재활용하면서 계산할 수 있다.
그러면 FFT를 하기 전에 $A$를 정렬 해보자.
정렬을 하기 위해 자기 위치를 찾아가는 과정은 각 수열의 길이가 짝수/홀수일 때 나눠서 따라가 보면 알 수 있다.
vector<complex<double>> b(a);
for (int i = 0; i < n; i++) {
int len = n, startIdx = 0, idx = i;
for(int len = n; len > 1; len >>= 1) {
if (idx & 1) startIdx += len >> 1;
idx >>= 1;
}
a[startIdx + idx] = b[i];
}
이렇게 결괏값이 ${A_0, A_1, A_2, ..., A_{N-1}}$이 될 수 있도록 A를 미리 정렬을 해두면 재귀적인 과정에서 $A_{even}, A_{odd}$를 할당하지 않아도 된다. 많이 좋아졌지만 더 욕심을 내서 정렬할 때 사용되는 b의 메모리 $O(n)$도 아까우니 이것도 없애보자.
$A_k$가 어디로 가는지 k를 2진수로 추적해보면 힌트가 보인다.
- $A_{000} => 0번째(000)$
- $A_{001} => 4번째(100)$
- $A_{010} => 2번째(010)$
- $A_{011} => 6번째(110)$
- $A_{100} => 1번째(001)$
- $A_{101} => 5번째(101)$
- $A_{110} => 3번째(011)$
- $A_{111} => 7번째(111)$
이를 보면 k는 k를 2진수로 변환했을 때 비트를 뒤집은 위치로 간다는 것을 알 수 있다.
k는 reverse(k)로 가고 reverse(k)는 reverse(reverse(k)), 즉 k로 간다. 따라서 단순히 k와 reverse(k)만 swap 하면 추가 메모리 없이 A를 정렬할 수 있다.
완성된 코드는 다음과 같다.
// a의 크기는 2^N 이어야 하고, IDFT의 경우 inverse = true로 넘김
void fft(vector<complex<double>> &a, bool inverse) {
int n = a.size();
// 메모리 재활용을 위한 정렬
for(int i = 0; i < n; i++) {
int rev = 0;
for(int j = 1, target = i; j < n; j <<= 1, target >>= 1) {
rev = (rev << 1) + (target & 1);
}
if(i < rev) {
swap(a[i], a[rev]);
}
}
for(int len = 2; len <= n; len <<= 1) {
double x = 2 * M_PI / len * (inverse ? -1 : 1);
complex<double> diff(cos(x), sin(x));
for(int i = 0; i < n; i += len) {
complex<double> e(1);
for(int j = 0; j < len/2; j++) {
int cur = i + j;
complex<double> even = a[cur];
complex<double> oddE = a[cur + len/2] * e;
a[cur] = even + oddE;
a[cur + len/2] = even - oddE;
e *= diff;
}
}
}
if(inverse) {
for(int i = 0; i < n; i++) {
a[i] /= n;
}
}
}'알고리즘' 카테고리의 다른 글
| 투셋(2-sat) (0) | 2019.10.18 |
|---|---|
| Manacher's Algorithm (0) | 2019.10.17 |
| 푸리에 변환(Fourier Transform) (1) | 2019.10.17 |
| 오일러 피 함수(Euler's phi function) (2) | 2019.10.17 |
| 모듈러 나눗셈 (0) | 2019.10.17 |




댓글