바둑에서는 한 수를 두었을 때 그 수의 승률을 판단해야 하는데, 이후에 벌어지는 모든 경우의 수를 탐색할 수가 없다. 이럴 때 몬테카를로(Monte Carlo) 방법을 사용한다. 모든 탐색은 못하지만 빠르게 랜덤 탐색을 반복하면서 통계적인 수치를 얻는 방법이다.
몬테카를로 방법
가장 쉬운 예로 $\pi$를 구하는 방법이 있다. 임의의 정사각형에 점을 찍어 원 안에 포함되는지 판단하는 빠른 탐색을 반복하여 통계적인 $\pi$의 값을 알 수 있다. 실행 횟수를 높일수록 실제 $\pi$값과 일치해가는 것을 볼 수 있다.

# 총 개수 -> 원 안에 있는 개수 / 총 개수 * 4
10 -> 2.8
100 -> 3.16
1000 -> 3.028
10000 -> 3.1504
100000 -> 3.13844
1000000 -> 3.143232바둑에 적용
하지만 바둑은 형세판단을 하기 위해 몬테카를로 방법을 많이 해도 기대한 값을 얻을 수 없다.
예를 들면 내 차례에 어떤 한 수를 두면 절대적으로 이길 수 있는 수가 있을 때, 몬테카를로 방법은 그런 중요도에 가치를 두지 않는다. 악수와 구분 없이 랜덤 하게 시도한다. 이를 무작위 랜덤이 아닌 좋은 수 위주로 탐색을 해서 통계를 내도록 조정해야 한다.
아래 순서는 이를 고려한 약간 변형된 몬테카를로 탐색 방법이다.
- Selection
루트에서 마지막 노드까지 탐색하며 내려간다. 자식 선택 기준은 승률이 높으면서 시도 횟수가 적은 노드를 선택함으로써 안정적인 탐색을 유도한다. 이 두 가지는 게임 탐색에 있어 발생하는 트레이드오프로 적절한 수식을 만들어 설정해야 한다. - Expension
횟수가 $n$이상이면 새로운 노드를 확장한다. - Evalutaion
끝까지 게임을 진행한다. 이때는 그럴듯한 다음 수를 빠르게 예측하는 롤 아웃 방법으로 두며 종국 한다. - Backup
게임 결과를 트리의 부모 노드들에게 반영한다.
기존 몬테카를로 방법에서는 좋은 한 수가 있을 때에도 다른 수와 같은 수준의 랜덤으로 탐색했다면, 이 방법은 그 좋은 수가 자주 선택되고, 확장되어 더 많은 탐색을 해서 통계가 많이 쌓인다. 따라서 인간이 기대하는 승률에 더 근접한 결과가 나온다.
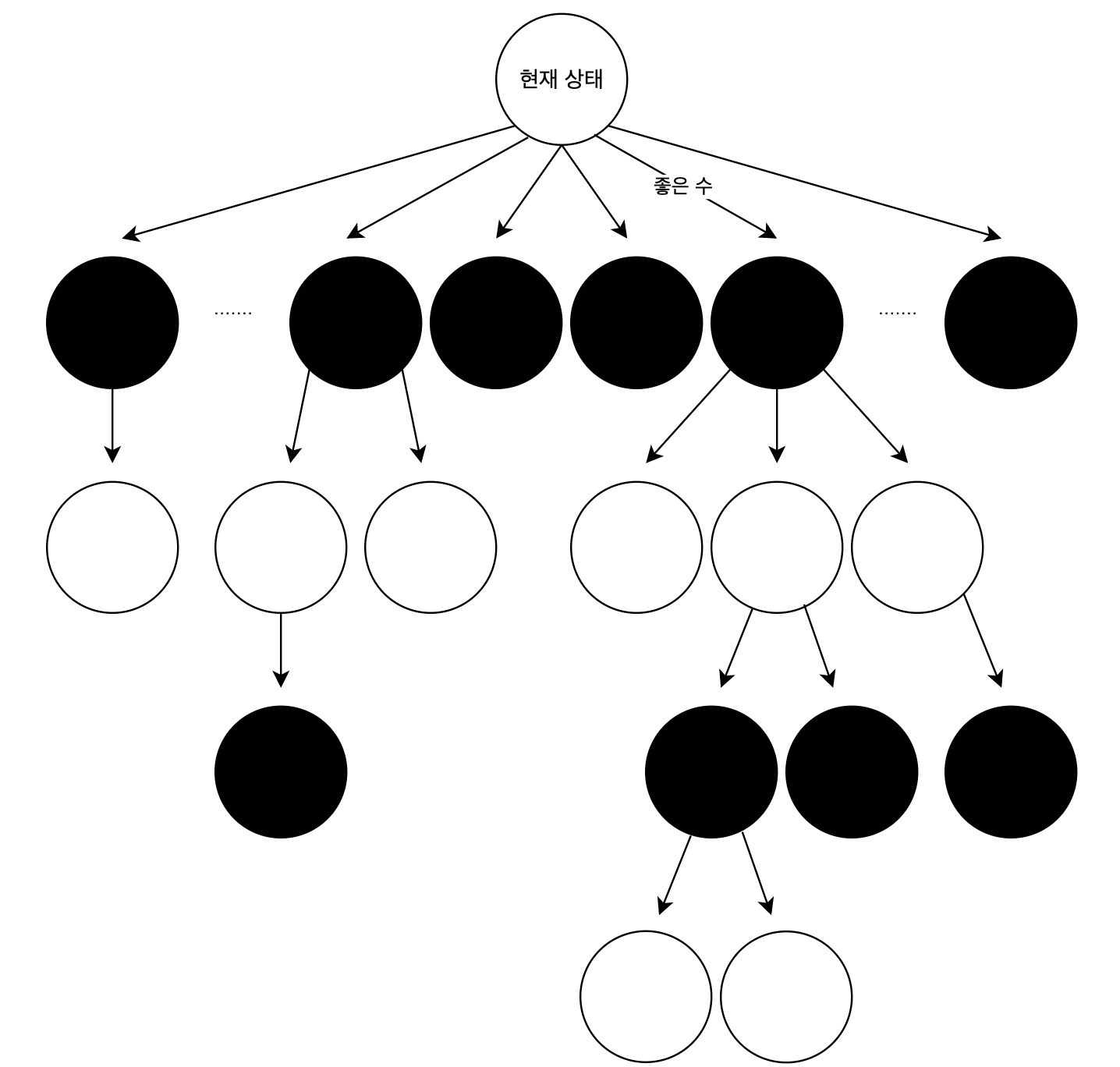
현재 내 차례에 좋은 수가 있다면 그 수의 선택 비율이 높아지면서 다른 수에 비해 깊게 탐색한다.
그러면 이렇게 몬테카를로 트리를 만든 후 실제 다음 수는 어떻게 정하는 게 좋을까? 승률이 높은 수를 택하는 것도 일리 있고, 탐색 횟수가 많았던 수를 택하는 것도 일리가 있다. 탐색 횟수가 무한하다면 두 후보가 일치함이 보장되지만 위 방법대로 자원의 한계가 있는 상태면 충분히 다를 수 있다. 이 경우에는 탐색 횟수가 많은 수가 더 좋다고 알려져서 이 수를 다음 수로 선택한다.
'딥러닝' 카테고리의 다른 글
| Keras로 모델 저장, 불러오기 (0) | 2019.11.16 |
|---|---|
| Keras로 간단한 CNN 구현하기 (0) | 2019.11.13 |
| 알파고의 강화학습 (0) | 2019.11.03 |
| 강화학습의 종류 (0) | 2019.11.03 |
| 알파고의 원리와 그 버전들 (0) | 2019.11.03 |




댓글